Phương trình bậc 2 là một kiến thức cơ bản mà đa số chúng ta đã được học từ thời cấp 2. Từ những nguyên tắc cơ bản đến những ứng dụng phức tạp, phương trình bậc 2 không chỉ là một khái niệm toán học trừu tượng, mà còn mang trong mình những giá trị thực tiễn vô cùng quan trọng. Nhưng bạn đã từng tự hỏi cách giải phương trình bậc 2 là gì và tại sao nó lại được sử dụng phổ biến đến vậy? Trong bài viết này, https://bangdaihochinhquy.com sẽ cùng nhau khám phá phương pháp tìm nghiệm phương trình bậc 2 từ những kiến thức cơ bản cho đến ứng dụng thực tiễn.
A. Lý thuyết về công thức nghiệm của phương trình bậc 2
1. Công thức nghiệm:
Đối với phương trình có dạng ax² + bx + c = 0 (a ≠ 0)
Ta có biệt thức của phương trình là: Δ = b2 – 4ac
- Trường hợp 1: Nếu Δ > 0 thì ta có phương trình có 2 nghiệm phân biệt
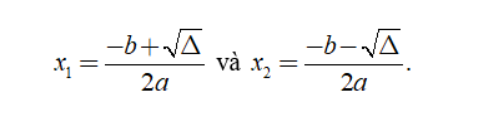
- Trường hợp 2: Nếu Δ = 0 thì ta có phương trình có nghiệm kép
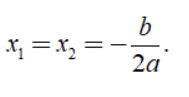
- Trường hợp 3: Nếu Δ < 0 thì ta có phương trình đã cho vô nghiệm
Lưu ý: Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có 2 ẩn a và c trái dấu, tức là ac < 0. Lúc này, ta có Δ = b² – 4ac > 0 ⇒ Phương trình luôn luôn có 2 nghiệm phân biệt
2. Định lý Viet của phương trình bậc 2
Khi gặp các phương trình bậc 2 hay giải phương trình bậc 2 một ẩn, các em học sinh không thể không nhắc tới định lý Viet. Đây là một trong những định lý quan trọng giúp các em dễ dàng giải quyết các dạng bài liên quan tới phương trình bậc 2
Ta có phương trình bậc 2 có dạng: ax² + bx + c = 0 (a ≠0) là phương trình có tối đa 2 nghiệm, gọi là x1 và x2. Khi đó, theo định lý Viet ta có mối liên hệ giữa các 2 nghiệm và các ẩn của phương trình như sau:
x1 + x2 = -b/a
x1x2 = c/a
Khi làm các dạng bài tập về phương trình bậc 2, các em học sinh có thể áp dụng mối liên hệ trên vào quá trình biến đổi biểu thức phương trình bậc 2 . Cụ thể như sau:
Bạn cũng có thể áp dụng định lý Viet đảo với 2 số x1 và x2 thỏa mãn 2 điều kiện:
- x1 + x2 = S
- x1x2 = P
Trong đó: cả x1 và x2 đều là nghiệm của phương trình x² – Sx + P = 0.
Ứng dụng của định lý Viet được áp dụng rất nhiều trong các dạng bài tập về phương trình bậc 2. Với phương trình bậc 2, các em học sinh hoàn toàn có thể dễ dàng tìm ra nghiệm của phương trình mà không cần dùng tới Δ trong một số trường hợp đặc biệt sau:
- Trường hợp 1: a+b+c=0 thì phương trình bậc 2 có 2 nghiệm là x1 = 1 và x2 = c/a.
- Trường hợp 2: a-b+c=0 thì phương trình bậc 2 2 nghiệm là x1 = -1 và x2 = -c/a. (Đây là trường hợp ngược lại với trường hợp 1, các em học sinh cần lưu ý kỹ để tránh bị nhầm lẫn trong quá trình làm bài)
Xem thêm :