Trong chương trình Toán học phổ thông, hình thoi là một dạng hình học quen thuộc nhưng lại khiến nhiều học sinh nhầm lẫn khi làm bài tập. Nguyên nhân không nằm ở công thức quá khó, mà chủ yếu do chưa hiểu rõ bản chất của hình thoi và mối liên hệ giữa các yếu tố của nó. Vì vậy, trước khi đi sâu vào cách tính chu vi và diện tích hình thoi, phần 1 của bài viết này sẽ giúp bạn hiểu đúng – nhớ lâu – áp dụng chính xác, thông qua phân tích chi tiết và ví dụ cụ thể.
Hình thoi là gì? Hiểu đúng trước khi tính
1.Định nghĩa hình thoi
Hình thoi là một tứ giác có bốn cạnh bằng nhau. Đây là đặc điểm quan trọng nhất và cũng là yếu tố giúp phân biệt hình thoi với các hình tứ giác khác.
Nói cách khác:
Nếu một tứ giác có 4 cạnh bằng nhau → đó là hình thoi Hình thoi không bắt buộc có góc vuông
👉 Rất nhiều học sinh nhầm lẫn rằng hình thoi phải giống hình vuông. Thực tế, hình vuông chỉ là một trường hợp đặc biệt của hình thoi khi các góc đều bằng 90 độ.
2. Các tính chất quan trọng của hình thoi
Để tính chu vi và diện tích hình thoi chính xác, bạn cần nhớ các tính chất sau:
Bốn cạnh bằng nhau Hai đường chéo: Cắt nhau tại trung điểm Vuông góc với nhau Hai góc đối bằng nhau Hình thoi là một dạng đặc biệt của hình bình hành
👉 Chính hai đường chéo vuông góc là chìa khóa giúp ta tính diện tích hình thoi một cách rất đơn giản.
Cách tính chu vi hình thoi – Dễ hơn bạn nghĩ
2.1. Bản chất của chu vi hình thoi
Chu vi là tổng độ dài các cạnh bao quanh hình.
Vì hình thoi có 4 cạnh bằng nhau, nên việc tính chu vi trở nên cực kỳ đơn giản.
Nếu gọi:
a là độ dài một cạnh của hình thoi
Thì:
(Chu vi hình thoi) P = a + a + a + a = 4a
2.2. Công thức tính chu vi hình thoi
(Chu vi hình thoi) P=4a
Trong đó:
a: độ dài một cạnh của hình thoi
📌 Lưu ý quan trọng:
Công thức này chỉ áp dụng khi bạn biết độ dài cạnh, không áp dụng trực tiếp khi đề bài chỉ cho đường chéo.
2.3. Ví dụ 1: Tính chu vi hình thoi cơ bản
Bài toán:
Một hình thoi có cạnh dài 7 cm. Tính chu vi hình thoi đó.
Giải:
Áp dụng công thức:
P = 4 x 7 = 28 cm
👉 Chu vi hình thoi bằng 28 cm
2.4. Ví dụ 2: Bài toán thực tế
Một mảnh đất có dạng hình thoi, mỗi cạnh dài 15 m. Người ta muốn rào xung quanh mảnh đất này. Hỏi cần bao nhiêu mét dây rào?
Phân tích:
Mảnh đất có dạng hình thoi Chu vi chính là tổng chiều dài hàng rào cần dùng
Giải:
P = 4 c 15 = 60 m
👉 Cần 60 mét dây rào để rào kín mảnh đất
2.5. Sai lầm thường gặp khi tính chu vi hình thoi
❌ Nhầm cạnh với nửa đường chéo
❌ Dùng công thức chu vi hình chữ nhật
❌ Lấy tổng hai đường chéo để tính chu vi
✅ Cách tránh sai:
Kiểm tra đề bài có cho độ dài cạnh hay không Nếu chưa cho cạnh, chưa thể tính chu vi ngay
3. Liên hệ giữa hình thoi và các hình khác
Hiểu mối liên hệ này giúp bạn nhớ công thức lâu hơn:
Hình thoi ⊂ Hình bình hành Hình vuông ⊂ Hình thoi Chu vi hình thoi = Chu vi hình vuông (nếu cùng độ dài cạnh)
👉 Nhờ đó, khi đã quen với chu vi hình vuông, bạn sẽ thấy chu vi hình thoi hoàn toàn không khó.
Bài viết liên quan:
- Công thức tính diện tích tam giác: vuông, thường, cân, đều
- Công thức tính diện tích hình thang: thường, vuông, cân
Bản chất diện tích hình thoi
1.Diện tích là gì?
Diện tích là phần mặt phẳng mà hình chiếm chỗ.
Với hình chữ nhật hay hình vuông, ta quen với công thức “dài × rộng”.
Tuy nhiên, hình thoi không có chiều dài – chiều rộng rõ ràng, vì các cạnh bị nghiêng.
👉 Chính vì vậy, diện tích hình thoi không tính theo cạnh, mà tính thông qua hai đường chéo.
1.2. Vai trò của hai đường chéo trong hình thoi
Hình thoi có hai đường chéo với các đặc điểm quan trọng:
Hai đường chéo vuông góc với nhau Cắt nhau tại trung điểm mỗi đường Chia hình thoi thành 4 tam giác vuông bằng nhau
👉 Đây chính là “chìa khóa” để xây dựng công thức tính diện tích hình thoi.
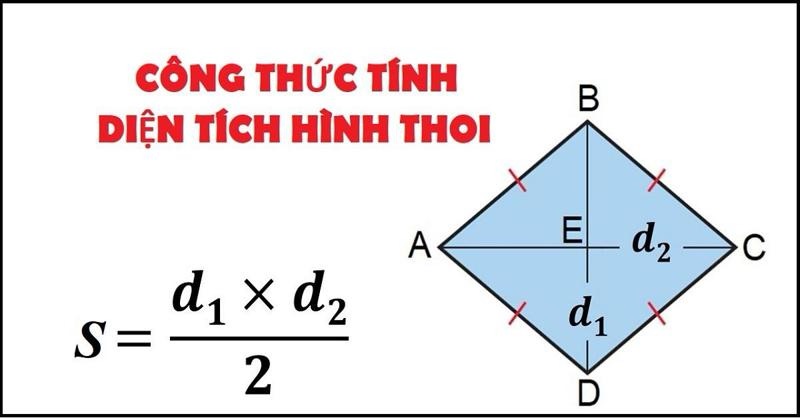
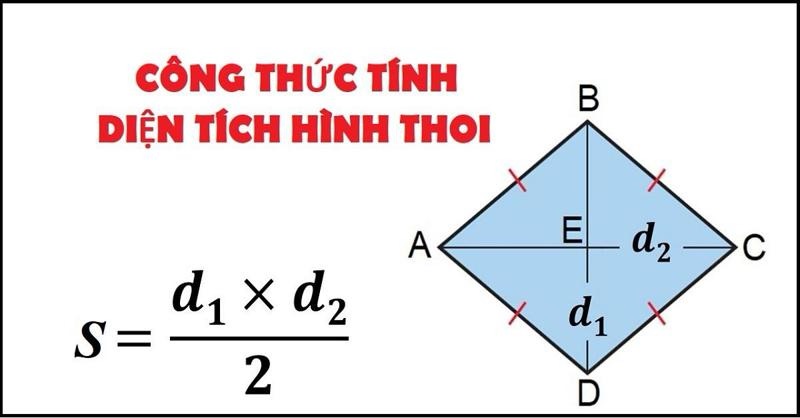
2. Công thức tính diện tích hình thoi
2.1. Công thức chuẩn
(Diện tích hình thoi) S=1/2 (d1d2)
Trong đó:
d1: độ dài đường chéo thứ nhất
d2: độ dài đường chéo thứ hai
📌 Công thức này đúng cho mọi hình thoi, không phụ thuộc vào góc nghiêng hay độ dài cạnh.
2.2. Vì sao lại chia cho 2?
Khi hai đường chéo cắt nhau vuông góc, chúng tạo thành 4 tam giác vuông.
Nếu ghép 2 tam giác vuông lại, ta được một hình chữ nhật có:
Chiều dài = d1 Chiều rộng = d2 / 2
Hoặc hiểu đơn giản hơn:
d1d2 là diện tích của hình chữ nhật “bao ngoài” Hình thoi chỉ chiếm một nửa diện tích đó
👉 Vì vậy, ta phải chia cho 2.
3. Ví dụ cơ bản về tính diện tích hình thoi
Ví dụ 1: Bài toán trực tiếp
Bài toán:
Một hình thoi có hai đường chéo lần lượt là 6 cm và 8 cm. Tính diện tích hình thoi.
Giải:
S = 1/2(6×8)= 24 cm
👉 Diện tích hình thoi là 24 cm²
Ví dụ 2: Bài toán gắn với thực tế
Bài toán:
Một tấm gạch trang trí có dạng hình thoi. Hai đường chéo của tấm gạch dài 20 cm và 30 cm. Hỏi diện tích tấm gạch là bao nhiêu?
Giải:
S = 1/2 (20×30)= 300 cm2
👉 Diện tích tấm gạch là 300 cm²
4. Ví dụ nâng cao: Khi đề bài cho nửa đường chéo
Đây là dạng bài rất hay gây nhầm lẫn trong các bài kiểm tra.
Ví dụ 3: Đề bài cho nửa đường chéo
Bài toán:
Một hình thoi có hai nửa đường chéo dài 5 cm và 7 cm. Tính diện tích hình thoi.
Phân tích:
Đường chéo thứ nhất: 5 x 2 = 10 cm Đường chéo thứ hai: 7 x 2 = 14 cm
Giải:
S = 1/2(10 x 14)= 70 cm²
👉 Diện tích hình thoi là 70 cm²
📌 Lưu ý cực kỳ quan trọng:
Nếu đề bài cho nửa đường chéo, bạn phải nhân đôi trước khi áp dụng công thức.
5. Những lỗi sai thường gặp khi tính diện tích hình thoi
❌ Dùng công thức diện tích hình bình hành
❌ Lấy cạnh nhân với đường chéo
❌ Quên chia cho 2
❌ Không nhận ra đề bài cho nửa đường chéo
✅ Cách tránh sai:
Xác định rõ đề bài cho đường chéo hay nửa đường chéo Nhớ đúng công thức: S = 1/2(d1d2)
1. Dạng 1: Tính chu vi và diện tích khi biết cạnh và đường chéo
Ví dụ 1: Bài toán tổng hợp cơ bản
Bài toán:
Một hình thoi có cạnh dài 10 cm, hai đường chéo lần lượt là 12 cm và 16 cm.
a) Tính chu vi hình thoi
b) Tính diện tích hình thoi
Lời giải:
a) Chu vi hình thoi
P = 4 x10 = 40 cm
b) Diện tích hình thoi
S = 1/2(12 x 16)= 96 cm2
👉 Đây là dạng bài “đủ dữ kiện”, chỉ cần nhớ đúng công thức là làm được ngay.
2. Dạng 2: Bài toán suy luận – tìm cạnh từ đường chéo
Đây là dạng bài nâng cao hơn, đòi hỏi học sinh phải kết hợp kiến thức về tam giác vuông.
2.1. Cơ sở lý thuyết
Hai đường chéo hình thoi:
Vuông góc với nhau Cắt nhau tại trung điểm
👉 Mỗi cạnh hình thoi chính là cạnh huyền của tam giác vuông tạo bởi:
Nửa đường chéo thứ nhất Nửa đường chéo thứ hai
Ví dụ 2: Tìm chu vi khi chỉ biết đường chéo
Bài toán:
Một hình thoi có hai đường chéo dài 10 cm và 24 cm. Tính chu vi hình thoi.
Phân tích:
Nửa đường chéo thứ nhất: 5 cm Nửa đường chéo thứ hai: 12 cm
Áp dụng định lý Pythagore để tính cạnh:
a = √(52+122 ) =√169= 13cm
Lời giải:
P = 4 x 13 = 52 cm
👉 Đây là dạng bài rất hay gặp trong đề thi, cần nhớ:
Muốn tính chu vi → phải tìm được cạnh.
3. Dạng 3: Bài toán thực tế gắn với hình thoi
Ví dụ 3: Ứng dụng thực tế
Bài toán:
Một khu vườn có dạng hình thoi, hai đường chéo dài 20 m và 30 m.
a) Tính diện tích khu vườn
b) Nếu rào xung quanh khu vườn, biết mỗi cạnh dài 18 m, hỏi cần bao nhiêu mét hàng rào?
Lời giải:
a) Diện tích khu vườn
S = 1/2 (20 x30)= 300 m2
b) Chu vi khu vườn
P = 4×18 = 72cm
👉 Các bài toán thực tế giúp học sinh hiểu rõ ý nghĩa của chu vi và diện tích, không chỉ là con số khô khan.
4. Dạng 4: Bài toán so sánh diện tích
Ví dụ 4: So sánh hình thoi và hình vuông
Bài toán:
Một hình thoi và một hình vuông có cùng chu vi là 40 cm. Biết hình vuông có cạnh 10 cm. Hỏi diện tích hình nào lớn hơn?
Lời giải:
Chu vi = 40 cm → hình thoi cũng có cạnh 10 cm Diện tích hình vuông:
Svuông= 10 x10 = 100 cm2
Diện tích hình thoi phụ thuộc vào đường chéo, không thể lớn hơn hình vuông khi cùng cạnh
👉 Hình vuông có diện tích lớn nhất trong các hình thoi có cùng chu vi.
5. Cách làm nhanh bài toán hình thoi
5.1. Quy trình 4 bước
Xác định đề bài hỏi chu vi hay diện tích Kiểm tra dữ kiện: Có cạnh không? Có đường chéo không? Chọn đúng công thức Kiểm tra đơn vị đo
6. Tổng kết toàn bộ bài viết
Sau 3 phần, bạn cần ghi nhớ chắc chắn:
📌 Chu vi hình thoi
P = 4a
📌 Diện tích hình thoi
S = 1/2(d1d2)
📌 Kiến thức nâng cao
Hai đường chéo vuông góc Cạnh là cạnh huyền của tam giác vuông Hình vuông là hình thoi đặc biệt
🎯 KẾT LUẬN:
Chỉ cần hiểu đúng bản chất và luyện tập theo từng dạng bài, bạn sẽ thấy chu vi và diện tích hình thoi không hề khó. Bài toán nào cũng có “đường đi”, quan trọng là bạn nhìn đúng bản chất hình học